Curso no ICTP-SAIFR busca ensinar e divulgar métodos numéricos espectrais

George Rawitscher, da Universidade de Connecticut, está ministrando um curso sobre esses métodos computacionais para a solução numérica de equações complexas

Métodos numéricos espectrais são o tema de um curso de um mês de duração que está sendo realizado pelo ICTP-SAIFR e ministrado por George Rawitscher, da Universidade de Connecticut. As aulas, que começaram dia 18 de março e vão até 15 de abril, são abertas a todos os interessados e tem como principal objetivo divulgar e ensinar esses métodos computacionais de resolver equações complexas, que embora criados na década de 70, ainda não são muito conhecidos e utilizados pela comunidade científica.

“Estou muito feliz com essa oportunidade de falar sobre métodos numéricos espectrais aqui no Brasil”, diz Rawitscher, que tem uma conexão especial com o país por ter feito sua graduação na Universidade de São Paulo (USP). “Eles são mais precisos e mais rápidos que outros geralmente utilizados, como os métodos numéricos à diferença finita e a elementos finitos”.

O curso abordará as principais propriedades dos métodos espectrais e várias de suas aplicações, com ênfase na resolução da equação de Schroedinger para problemas de uma dimensão.

Precisão

A principal diferença e vantagem dos métodos espectrais é sua precisão.

Para resolver equações diferenciais ou integrais, por exemplo, os métodos computacionais fazem aproximações, pois precisam transformar um espaço contínuo, com infinitos pontos, em um espaço discreto, com um número finito de pontos. Os métodos de diferença finita e elementos finitos precisam levar em consideração um número muito maior de pontos desse espaço para terem a mesma exatidão dos métodos espectrais.

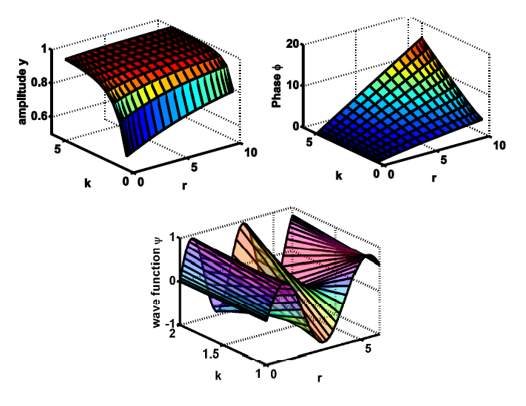
Métodos espectrais podem ser utilizados para obter uma função de onda a partir do cálculo de sua amplitude e de sua fase.

A cada cálculo, devido à precisão de apenas 8 casas decimais da maior parte dos computadores, surgem erros de arredondamento, que vão se acumulando. Métodos espectrais diminuem esses erros e conseguem obter um resultado bem mais preciso. A principal desvantagem do método é o fato de ser mais complexo e mais difícil de ser ensinado aos alunos.

“Métodos espectrais não usam matrizes esparsas, como os demais”, diz Rawitscher. “As matrizes desse método são não-esparsas, e por isso eles requerem um maior conhecimento sobre matemática para serem dominados. Entretanto, além de serem mais precisos, esses métodos podem ser também mais rápidos. Para obter um resultado com uma precisão semelhante, os métodos espectrais podem ser até 20 vezes mais rápidos”.

Aplicações

O curso de Rawitscher focará principalmente nas aplicações dos métodos espectrais na área de Física, especialmente para resolver a equação de Schroedinger para problemas de uma dimensão. Entretanto, esses métodos podem ter diversas outras aplicações. Ainda dentro da Física, ele pode ser usado na resolução de problemas quânticos que buscam estudar as interações entre átomos que estão distantes entre si.

Já um exemplo de aplicação fora da Física está na área de Geologia: os métodos espectrais podem ser usados para calcular como ondas que causam terremotos se propagam pela Terra. Na Medicina, segundo Rawitscher, os métodos também podem ser usados na análise de dados de exames de tomografia.

“Métodos de diferença finita e elementos finitos são bons, mas foram superados pelos métodos espectrais”, afirma Rawitscher. “Gostaria de popularizar esses métodos na comunidade científica, e esse curso é uma oportunidade para isso”.